11258. Количество прямоугольников

Сетка состоит из n * m единичных квадратов. Сколько различных прямоугольников можно изобразить на ней?

Стороны прямоугольников должны быть параллельны линиям сетки. Прямоугольник должен покрывать целое число полных квадратов. Два прямоугольника одинакового размера считаются разными, если они расположены в разных местах сетки.

Вход. Два целых числа n и m (n, m ≤ 10⁵).

Выход. Выведите количество различных прямоугольников, которые можно изобразить на сетке.

Пример входа	Пример выхода
2 3	18

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Расмотрим размер прямоугольника a * b, изображенного на сетке. Рассмотрим, сколькими способами можно выбрать значение a. Сетка содержит n строк квадратов, следовательно в сетке имеется n + 1 горизонтальная линия. Пронумеруем их числами от 1 до n + 1. Выберем две линии i и j (i < j). Проведем между ними отрезок – это и будет вертикальная сторона прямоугольника a. Количество способов выбрать два числа i и j (i < j) из множества {1, 2, …, n + 1} равно . Например, для n = 2 имеется 3 варианта выбрать вертикальную сторону прямоугольника:

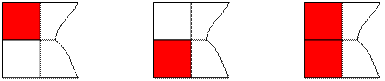
Аналогично, в сетке имеется m + 1 вертикальная линия. Количество способов выбрать горизонтальную сторону прямоугольника равно .

Следовательно количество различных прямоугольников на сетке равно

* =

Пример

Для прямоугольника 2 * 3 имеются:

· 6 единичных прямоугольников;

· 4 прямоугольника размером 1 * 2;

· 2 горизонтальных прямоугольника 1 * 3;

· 3 вертикальных прямоугольника 2 * 1;

· 2 прямоугольника 2 * 2;

· 1 прямоугольник 2 * 3;

Итого получилось * = 3 * 6 = 18 прямоугольников.

Реализация алгоритма

Поскольку n, m ≤ 10⁵, то количество прямоугольников может достигать * ≤ (10⁵)² * (10⁵)² = 10²⁰. Этот результат выходит за пределы 64 битового целого числа. Поэтому реализуем решение на языке Питон.

n, m = map(int,input().split())

a = (n + 1) * n // 2

b = (m + 1) * m // 2

res = a * b

print(res)